We summarize the performance characteristics of classic algorithms anddata structures for sorting, priority queues, symbol tables, and graph processing.
- Python Algorithm Cheat Sheet
- Algorithm Cheat Sheet Pdf
- Data Structures And Algorithms Cheat Sheet Github
- Data Structures And Algorithms Cheat Sheet 2020
- Computer Science Data Structures And Algorithms Cheat Sheet
- Data Structures And Algorithms Cheat Sheet
Algorithms and Data Structures Cheatsheet 11/5/20, 9:06 PM Page 2 of 10 k common logarithm such that log 10.
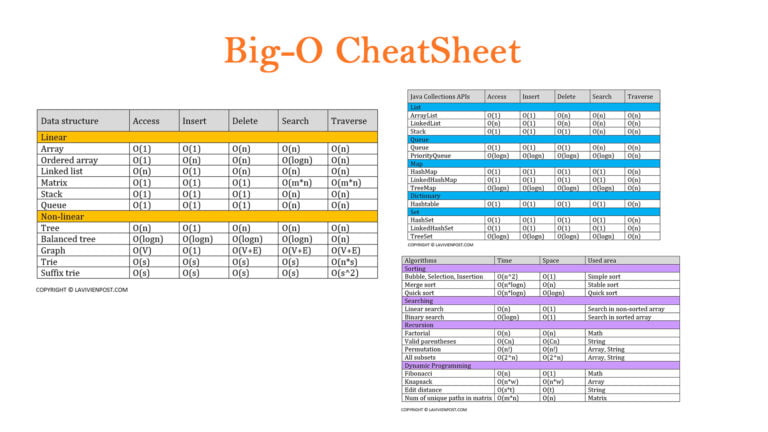
- Big-O Cheat Sheet for Some Data Structures and Algorithms.
- . Boolean: It is a built-in data type that can take the values TRUE or FALSE Primitive Data Structures:. Integer: It is used to represent numeric data, more specifically whole numbers from negative infinity to infinity. Eg: 4, 5, -1 etc. Float: It stands for floating point number. Eg: 1.1,2.3,9.3etc.
We also summarize some of the mathematics useful in the analysis of algorithms, including commonly encountered functions;useful formulas and appoximations; properties of logarithms;asymptotic notations; and solutions to divide-and-conquer recurrences.
Sorting.
The table below summarizes the number of compares for a variety of sortingalgorithms, as implemented in this textbook.It includes leading constants but ignores lower-order terms.| ALGORITHM | CODE | STABLE | BEST | AVERAGE | WORST | REMARKS | |
|---|---|---|---|---|---|---|---|
| selection sort | Selection.java | ✔ | ½ n 2 | ½ n 2 | ½ n 2 | n exchanges; quadratic in best case | |
| insertion sort | Insertion.java | ✔ | ✔ | n | ¼ n 2 | ½ n 2 | use for small or partially-sorted arrays |
| bubble sort | Bubble.java | ✔ | ✔ | n | ½ n 2 | ½ n 2 | rarely useful; use insertion sort instead |
| shellsort | Shell.java | ✔ | n log3n | unknown | c n 3/2 | tight code; subquadratic | |
| mergesort | Merge.java | ✔ | ½ n lg n | n lg n | n lg n | n log n guarantee; stable | |
| quicksort | Quick.java | ✔ | n lg n | 2 n ln n | ½ n 2 | n log n probabilistic guarantee; fastest in practice | |
| heapsort | Heap.java | ✔ | n† | 2 n lg n | 2 n lg n | n log n guarantee; in place | |
| †n lg n if all keys are distinct | |||||||
Priority queues.
The table below summarizes the order of growth of the running time ofoperations for a variety of priority queues, as implemented in this textbook.It ignores leading constants and lower-order terms.Except as noted, all running times are worst-case running times.| DATA STRUCTURE | CODE | INSERT | MIN | DELETE | MERGE | ||
|---|---|---|---|---|---|---|---|
| array | BruteIndexMinPQ.java | 1 | n | n | 1 | 1 | n |
| binary heap | IndexMinPQ.java | log n | log n | 1 | log n | log n | n |
| d-way heap | IndexMultiwayMinPQ.java | logdn | d logdn | 1 | logdn | d logdn | n |
| binomial heap | IndexBinomialMinPQ.java | 1 | log n | 1 | log n | log n | log n |
| Fibonacci heap | IndexFibonacciMinPQ.java | 1 | log n† | 1 | 1 † | log n† | 1 |
| † amortized guarantee | |||||||
Symbol tables.
The table below summarizes the order of growth of the running time ofoperations for a variety of symbol tables, as implemented in this textbook.It ignores leading constants and lower-order terms.| worst case | average case | ||||||
|---|---|---|---|---|---|---|---|
| DATA STRUCTURE | CODE | SEARCH | INSERT | DELETE | SEARCH | INSERT | DELETE |
| sequential search (in an unordered list) | SequentialSearchST.java | n | n | n | n | n | n |
| binary search (in a sorted array) | BinarySearchST.java | log n | n | n | log n | n | n |
| binary search tree (unbalanced) | BST.java | n | n | n | log n | log n | sqrt(n) |
| red-black BST (left-leaning) | RedBlackBST.java | log n | log n | log n | log n | log n | log n |
| AVL | AVLTreeST.java | log n | log n | log n | log n | log n | log n |
| hash table (separate-chaining) | SeparateChainingHashST.java | n | n | n | 1 † | 1 † | 1 † |
| hash table (linear-probing) | LinearProbingHashST.java | n | n | n | 1 † | 1 † | 1 † |
| † uniform hashing assumption | |||||||
Graph processing.
The table below summarizes the order of growth of the worst-case running time and memory usage (beyond the memory for the graph itself)for a variety of graph-processing problems, as implemented in this textbook.It ignores leading constants and lower-order terms.All running times are worst-case running times.| PROBLEM | ALGORITHM | CODE | TIME | SPACE |
|---|---|---|---|---|
| path | DFS | DepthFirstPaths.java | E + V | V |
| shortest path (fewest edges) | BFS | BreadthFirstPaths.java | E + V | V |
| cycle | DFS | Cycle.java | E + V | V |
| directed path | DFS | DepthFirstDirectedPaths.java | E + V | V |
| shortest directed path (fewest edges) | BFS | BreadthFirstDirectedPaths.java | E + V | V |
| directed cycle | DFS | DirectedCycle.java | E + V | V |
| topological sort | DFS | Topological.java | E + V | V |
| bipartiteness / odd cycle | DFS | Bipartite.java | E + V | V |
| connected components | DFS | CC.java | E + V | V |
| strong components | Kosaraju–Sharir | KosarajuSharirSCC.java | E + V | V |
| strong components | Tarjan | TarjanSCC.java | E + V | V |
| strong components | Gabow | GabowSCC.java | E + V | V |
| Eulerian cycle | DFS | EulerianCycle.java | E + V | E + V |
| directed Eulerian cycle | DFS | DirectedEulerianCycle.java | E + V | V |
| transitive closure | DFS | TransitiveClosure.java | V (E + V) | V 2 |
| minimum spanning tree | Kruskal | KruskalMST.java | E log E | E + V |
| minimum spanning tree | Prim | PrimMST.java | E log V | V |
| minimum spanning tree | Boruvka | BoruvkaMST.java | E log V | V |
| shortest paths (nonnegative weights) | Dijkstra | DijkstraSP.java | E log V | V |
| shortest paths (no negative cycles) | Bellman–Ford | BellmanFordSP.java | V (V + E) | V |
| shortest paths (no cycles) | topological sort | AcyclicSP.java | V + E | V |
| all-pairs shortest paths | Floyd–Warshall | FloydWarshall.java | V 3 | V 2 |
| maxflow–mincut | Ford–Fulkerson | FordFulkerson.java | EV (E + V) | V |
| bipartite matching | Hopcroft–Karp | HopcroftKarp.java | V ½ (E + V) | V |
| assignment problem | successive shortest paths | AssignmentProblem.java | n 3 log n | n 2 |
Commonly encountered functions.
Here are some functions that are commonly encounteredwhen analyzing algorithms.| FUNCTION | NOTATION | DEFINITION |
|---|---|---|
| floor | ( lfloor x rfloor ) | greatest integer (; le ; x) |
| ceiling | ( lceil x rceil ) | smallest integer (; ge ; x) |
| binary logarithm | ( lg x) or (log_2 x) | (y) such that (2^{,y} = x) |
| natural logarithm | ( ln x) or (log_e x ) | (y) such that (e^{,y} = x) |
| common logarithm | ( log_{10} x ) | (y) such that (10^{,y} = x) |
| iterated binary logarithm | ( lg^* x ) | (0) if (x le 1;; 1 + lg^*(lg x)) otherwise |
| harmonic number | ( H_n ) | (1 + 1/2 + 1/3 + ldots + 1/n) |
| factorial | ( n! ) | (1 times 2 times 3 times ldots times n) |
| binomial coefficient | ( n choose k ) | ( frac{n!}{k! ; (n-k)!}) |
Useful formulas and approximations.
Here are some useful formulas for approximations that are widely used in the analysis of algorithms.- Harmonic sum: (1 + 1/2 + 1/3 + ldots + 1/n sim ln n)
- Triangular sum: (1 + 2 + 3 + ldots + n = n , (n+1) , / , 2 sim n^2 ,/, 2)
- Sum of squares: (1^2 + 2^2 + 3^2 + ldots + n^2 sim n^3 , / , 3)
- Geometric sum: If (r neq 1), then(1 + r + r^2 + r^3 + ldots + r^n = (r^{n+1} - 1) ; /; (r - 1))
- (r = 1/2): (1 + 1/2 + 1/4 + 1/8 + ldots + 1/2^n sim 2)
- (r = 2): (1 + 2 + 4 + 8 + ldots + n/2 + n = 2n - 1 sim 2n), when (n) is a power of 2
- Stirling's approximation: (lg (n!) = lg 1 + lg 2 + lg 3 + ldots + lg n sim n lg n)
- Exponential: ((1 + 1/n)^n sim e; ;;(1 - 1/n)^n sim 1 / e)
- Binomial coefficients: ({n choose k} sim n^k , / , k!) when (k) is a small constant
- Approximate sum by integral: If (f(x)) is a monotonically increasing function, then( displaystyle int_0^n f(x) ; dx ; le ; sum_{i=1}^n ; f(i) ; le ; int_1^{n+1} f(x) ; dx)
Properties of logarithms.
- Definition: (log_b a = c) means (b^c = a).We refer to (b) as the base of the logarithm.
- Special cases: (log_b b = 1,; log_b 1 = 0 )
- Inverse of exponential: (b^{log_b x} = x)
- Product: (log_b (x times y) = log_b x + log_b y )
- Division: (log_b (x div y) = log_b x - log_b y )
- Finite product: (log_b ( x_1 times x_2 times ldots times x_n) ; = ; log_b x_1 + log_b x_2 + ldots + log_b x_n)
- Changing bases: (log_b x = log_c x ; / ; log_c b )
- Rearranging exponents: (x^{log_b y} = y^{log_b x})
- Exponentiation: (log_b (x^y) = y log_b x )
Aymptotic notations: definitions.
| NAME | NOTATION | DESCRIPTION | DEFINITION |
|---|---|---|---|
| Tilde | (f(n) sim g(n); ) | (f(n)) is equal to (g(n)) asymptotically (including constant factors) | ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 1) |
| Big Oh | (f(n)) is (O(g(n))) | (f(n)) is bounded above by (g(n)) asymptotically (ignoring constant factors) | there exist constants (c > 0) and (n_0 ge 0) such that (0 le f(n) le c cdot g(n)) forall (n ge n_0) |
| Big Omega | (f(n)) is (Omega(g(n))) | (f(n)) is bounded below by (g(n)) asymptotically (ignoring constant factors) | ( g(n) ) is (O(f(n))) |
| Big Theta | (f(n)) is (Theta(g(n))) | (f(n)) is bounded above and below by (g(n)) asymptotically (ignoring constant factors) | ( f(n) ) is both (O(g(n))) and (Omega(g(n))) |
| Little oh | (f(n)) is (o(g(n))) | (f(n)) is dominated by (g(n)) asymptotically (ignoring constant factors) | ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 0) |
| Little omega | (f(n)) is (omega(g(n))) | (f(n)) dominates (g(n)) asymptotically (ignoring constant factors) | ( g(n) ) is (o(f(n))) |
Common orders of growth.
| NAME | NOTATION | EXAMPLE | CODE FRAGMENT |
|---|---|---|---|
| Constant | (O(1)) | array access arithmetic operation function call | |
| Logarithmic | (O(log n)) | binary search in a sorted array insert in a binary heap search in a red–black tree | |
| Linear | (O(n)) | sequential search grade-school addition BFPRT median finding | |
| Linearithmic | (O(n log n)) | mergesort heapsort fast Fourier transform | |
| Quadratic | (O(n^2)) | enumerate all pairs insertion sort grade-school multiplication | |
| Cubic | (O(n^3)) | enumerate all triples Floyd–Warshall grade-school matrix multiplication | |
| Polynomial | (O(n^c)) | ellipsoid algorithm for LP AKS primality algorithm Edmond's matching algorithm | |
| Exponential | (2^{O(n^c)}) | enumerating all subsets enumerating all permutations backtracing search |
Asymptotic notations: properties.
- Reflexivity: (f(n)) is (O(f(n))).
- Constants: If (f(n)) is (O(g(n))) and ( c > 0 ),then (c cdot f(n)) is (O(g(n)))).
- Products: If (f_1(n)) is (O(g_1(n))) and ( f_2(n) ) is (O(g_2(n)))),then (f_1(n) cdot f_2(n)) is (O(g_1(n) cdot g_2(n)))).
- Sums: If (f_1(n)) is (O(g_1(n))) and ( f_2(n) ) is (O(g_2(n)))),then (f_1(n) + f_2(n)) is (O(max { g_1(n) , g_2(n) })).
- Transitivity: If (f(n)) is (O(g(n))) and ( g(n) ) is (O(h(n))),then ( f(n) ) is (O(h(n))).
- Polynomials: Let (f(n) = a_0 + a_1 n + ldots + a_d n^d) with(a_d > 0). Then, ( f(n) ) is (Theta(n^d)).
- Logarithms and polynomials: ( log_b n ) is (O(n^d)) for every ( b > 0) and every ( d > 0 ).
- Exponentials and polynomials: ( n^d ) is (O(r^n)) for every ( r > 0) and every ( d > 0 ).
- Factorials: ( n! ) is ( 2^{Theta(n log n)} ).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = c)for some constant ( 0 < c < infty), then(f(n)) is (Theta(g(n))).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 0),then (f(n)) is (O(g(n))) but not (Theta(g(n))).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = infty),then (f(n)) is (Omega(g(n))) but not (O(g(n))).
Here are some examples.

| FUNCTION | (o(n^2)) | (O(n^2)) | (Theta(n^2)) | (Omega(n^2)) | (omega(n^2)) | (sim 2 n^2) | (sim 4 n^2) |
|---|---|---|---|---|---|---|---|
| (log_2 n) | ✔ | ✔ | |||||
| (10n + 45) | ✔ | ✔ | |||||
| (2n^2 + 45n + 12) | ✔ | ✔ | ✔ | ✔ | |||
| (4n^2 - 2 sqrt{n}) | ✔ | ✔ | ✔ | ✔ | |||
| (3n^3) | ✔ | ✔ | |||||
| (2^n) | ✔ | ✔ |


Divide-and-conquer recurrences.
For each of the following recurrences we assume (T(1) = 0)and that (n,/,2) means either (lfloor n,/,2 rfloor) or(lceil n,/,2 rceil).| RECURRENCE | (T(n)) | EXAMPLE |
|---|---|---|
| (T(n) = T(n,/,2) + 1) | (sim lg n) | binary search |
| (T(n) = 2 T(n,/,2) + n) | (sim n lg n) | mergesort |
| (T(n) = T(n-1) + n) | (sim frac{1}{2} n^2) | insertion sort |
| (T(n) = 2 T(n,/,2) + 1) | (sim n) | tree traversal |
| (T(n) = 2 T(n-1) + 1) | (sim 2^n) | towers of Hanoi |
| (T(n) = 3 T(n,/,2) + Theta(n)) | (Theta(n^{log_2 3}) = Theta(n^{1.58...})) | Karatsuba multiplication |
| (T(n) = 7 T(n,/,2) + Theta(n^2)) | (Theta(n^{log_2 7}) = Theta(n^{2.81...})) | Strassen multiplication |
| (T(n) = 2 T(n,/,2) + Theta(n log n)) | (Theta(n log^2 n)) | closest pair |
Master theorem.
Let (a ge 1), (b ge 2), and (c > 0) and suppose that(T(n)) is a function on the non-negative integers that satisfiesthe divide-and-conquer recurrence$$T(n) = a ; T(n,/,b) + Theta(n^c)$$with (T(0) = 0) and (T(1) = Theta(1)), where (n,/,b) meanseither (lfloor n,/,b rfloor) or either (lceil n,/,b rceil).- If (c < log_b a), then (T(n) = Theta(n^{log_{,b} a}))
- If (c = log_b a), then (T(n) = Theta(n^c log n))
- If (c > log_b a), then (T(n) = Theta(n^c))
 Remark: there are many different versions of the master theorem. The Akra–Bazzi theoremis among the most powerful.
Remark: there are many different versions of the master theorem. The Akra–Bazzi theoremis among the most powerful.Last modified on September 12, 2020.
Copyright © 2000–2019Robert SedgewickandKevin Wayne.All rights reserved.
Hey Finxters! Do you know what time it is? That’s right! It’s time for some more cheat sheets!! These cheat sheets are meant to help you on your way to becoming a great Python developer and of course becoming one of the best Python freelancers globally! This article is all about algorithms used in software development and the cheat sheets we will use to do this. Let’s get started without further delay!
Cheat Sheet 1: Princeton
This cheat sheet is one you will want to bookmark as it is part of an ebook! It primarily focuses on Algorithm and Data Structures.The area I would like you to focus is ⅓ of the way down beginning at arrays. Consider bookmarking the book(I have!) Chapter 4 deep dives into algorithms and data structures. It includes a list of the Python code structures used throughout the chapter with complete explanations on what is happening and the how!
Pros: Perfect for deep diving into Algorithm coding in Python!
Cons: Part of an ebook
Cheat Sheet 2: AlgoDaily.com
This cheat sheet will go over the concepts of Big-O and Algorithmic complexity used in programming. Plus a video that discusses the concept! Algodaily is the place to be if you want to learn Algorithms and data structures for interviews to land a software career as a consultant or full time employee for a company.
Pros: Best place to learn everything you need to know for Algorithms and Data structures!
Cons: Does not have the ability to print, more structured towards interviews.
Cheat Sheet 3: Microsoft
This cheat sheet can be downloaded and pinned to the wall behind the monitor or place in your developers binder. It is carefully structured by microsoft to show you how to properly use algorithms for ML. Start in the What do you want to do box and you will be on your way to writing your algorithm!
Pros: Perfect place to start. It answers the question Where do I start?
Cons: None that I can see.
Cheat Sheet 4: Cheatography
This cheat sheet is all about sorting algorithms with boiler code included for bubble sorting, quicksort and selection. It presents a clear table of which is a method and which is a sorting algorithm. Print this one and keep it pinned to the wall or place it in your developers binder
Pros: Rated ‘E’ for everyone.
Cons: None that I can see.
Cheat Sheet 5: Medium
This cheat sheet is for learning the searching and sorting algorithms used in Python. It has code snippets, visuals on the different algorithms and explanations. This cheat sheet is on Medium, a fast up-coming developers source on information in the Development and IT field. Bookmark this page, since it doesn’t print.
Pros: Great place to begin learning sorting and searching algorithms.
Cons: You’ll have to subscribe to Medium to read this cheat sheet.
Cheat Sheet 6: Dummies
Here is another cheat sheet for you to bookmark, presented to you from the classic series How to for Dummies. It has tables for looking for, which has type, explanations and links for further explanations.
Pros: Perfect if you’re having a hard time understanding where to begin with your algorithms
Cons: Cannot be printed. Bookmark the page, I did.
Cheat Sheet 7: Packt
Python Algorithm Cheat Sheet
This is a pdf that you can print and pin to the wall behind the monitor! It has tables of the different algorithms, the data structures and graphs. Keep it handy when you are learning Big-O algorithms.
Pros: Rated ‘E’ for everyone.
Cons: You’ll have to go to Packt for the Big-O book to read.
Cheat Sheet 8: Analytics Vidhya
This cheat sheet is broken down into 2 sides with Python and R for machine learning algorithms for supervised, unsupervised and reinforcement learning. It has code examples to get you started for both languages.
Pros: Rated ‘E’ for everyone, contains 2 languages.
Cons: Save it as an image to your laptop before printing.
Cheat Sheet 9: Scikit Learn
Algorithm Cheat Sheet Pdf
This cheat sheet map uses Scikit Learn to point you towards the right estimator to try on your data sets.
Pros: Rated ‘E’ for everyone.
Cons: No code samples.
Data Structures And Algorithms Cheat Sheet Github
Cheat Sheet 10: SAS
Data Structures And Algorithms Cheat Sheet 2020
This cheat sheet is used to help point you towards the correct algorithm to use for your data sets. The tutorial found online. Which machine learning algorithm do I use will help you make the correct choice.
Pros: Rated ‘E’ for everyone.
Cons: None that I can see.
This is just some of the cheat sheets I have found online and there are a ton more!! It is important to really understand Machine learning algorithms so I encourage you to sign up for a library (Packt is great!) and read the books they have available! To get you started I added a book from Pearsons! This book is an Introduction to Programming with Python! It covers Python from its basics to the algorithms and data structures you need to get you started! Keep on becoming a great Pythoner! One code at a time!
Related Articles:
Computer Science Data Structures And Algorithms Cheat Sheet
While working as a researcher in distributed systems, Dr. Christian Mayer found his love for teaching computer science students.
To help students reach higher levels of Python success, he founded the programming education website Finxter.com. He’s author of the popular programming book Python One-Liners (NoStarch 2020), coauthor of the Coffee Break Python series of self-published books, computer science enthusiast, freelancer, and owner of one of the top 10 largest Python blogs worldwide.
His passions are writing, reading, and coding. But his greatest passion is to serve aspiring coders through Finxter and help them to boost their skills. You can join his free email academy here.
Data Structures And Algorithms Cheat Sheet
Related Posts
